色差仪卢瑟条件什么意思?色差仪为了要模拟标准观察者在标准照明体照明下观察到的物体颜色情况,色差仪的总光谱灵敏度必须符合卢瑟条件,卢瑟条件是校正滤色器设计的基础。那么,色差仪卢瑟条件怎么实现?本文做了介绍。

色差仪卢瑟条件什么意思?
光电测色仪是仿照人眼感色的原理原理制成的,采用了能感觉红、绿、蓝三种颜色的受光器,将各自所感受光电的光电流加以放大处理,得出各色的刺激量,从而获得这一颜色信号。这里使用的受光器是在可见光的波段中,具有平坦的感受特性的光电二极管(硅系)和能平坦地修正光谱敏感度特性的虑色器和能调整到符合人眼色觉的虑色镜。这里重要的是三块滤色镜能符合人眼的色觉程度,这种相互一致的条件称为卢瑟条件。
卢瑟条件最常用的修正方法是预先准备颜色稳定的若干色板作为标准色,用最接近式样颜色的色板进行测定并根据光电测色仪的测定值,与用分光光度计预先求得的标准差值进行修正。在光电测色仪上接上专用计算机,预先准备在各波段中修正卢瑟条件的程序,可以使工作效率提高,复杂程度减少,同时将各个滤色镜进行修正。
物体在10°视场、D65光源照射下,物体颜色三刺激值X、Y、Z由三刺激值标准方程式可推导出如下计算公式:
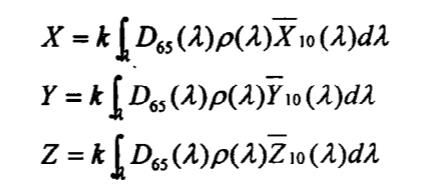
设计三组接收器使它模拟人眼的X、Y、Z三个感光机构,把人眼所接受的刺激用三组接收器所产生的光电流表示,则可以确定物体的颜色。在用某测色系统中,光源S(λ)按照一定的角度照射物体,用光电元件和滤色器配合的接收器在一定方向接收,则接收器上产生对应的光电流:
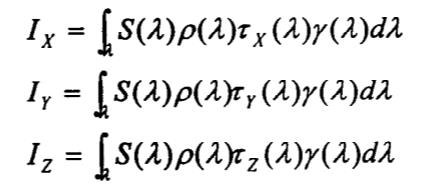
式中:τX(λ)、τY(λ)、τZ(λ)——仪器特定滤色器的光谱透过率;γ(λ)——仪器探测器的相对光谱响应度。比较上面的式子,如果满足下列条件即卢瑟条件(Luther condition):
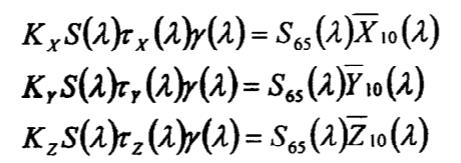
式中Kx、Ky、Kz是与波长无关的常数,则测色仪的总灵敏度特性与CIE规定的标准观察者的X、Y、Z一致,物体颜色三刺激值正比于光电流数值。
仪器符合卢瑟条件的完善程度,决定了仪器的测量精度。为了减少由于卢瑟条件不够满足而导致的测色误差,应为仪器配备适当的专用工作色板,用来分别校正仪器。对于满足卢瑟条件的仪器,仅配上工作白板即可。而对于偏离卢瑟条件较严重的仪器,应配足能覆盖相应测色范围的专用工作色板。
色差仪卢瑟条件实现方法:
测色仪的总灵敏度特性与CIE规定的标准观察者的X、Y、Z一致,物体颜色三刺激值正比于光电流数值,仪器符合卢瑟条件的完善程度,决定了仪器的测量精度。
为了进行光电积分式颜色测量,仪器的三个光探测器的光谱响应必须满足卢瑟条件。能够实现这种要求的方法通常有两种,即模板法和光学滤色片法。
1.模板法
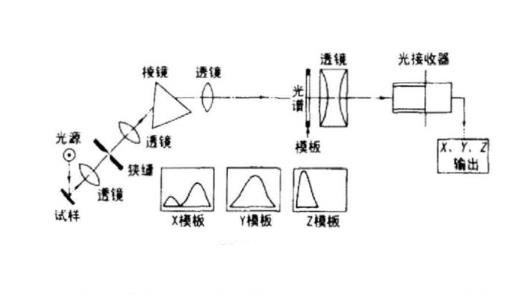
模板法采用模板使光探测器的光谱响应特性与CIE光谱三刺激值函数相匹配,即满足卢瑟条件的要求。下图是模板法光电积分式色度计的光学系统,光源照明测试样品,由试样表面反射的光辐射,通过透镜和棱镜色散成光谱;在光谱面上分别放置X模板、Y模板和Z模板,它们使光接收器对等能光谱的光谱响应,分别与CIE色度匹配函数x
(λ)、y(λ)和 z(λ)成正比;从模板透过的光谱能量,由透镜会聚于光接收器上,即可测出试样的CIE三刺激值X、Y、Z。
2.光学滤色片法
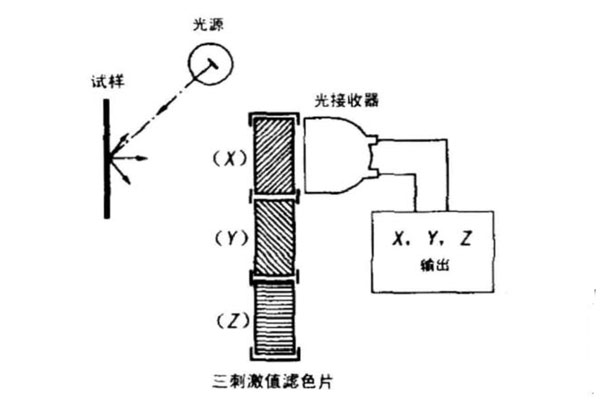
光学滤色片法不采用色散系统和光谱模板,而是利用有色玻璃片的组合来实现卢瑟条件。为使光探测器的相对光谱灵敏度S(λ)符合aE的色度匹配函数x(λ)、y(λ)、z(λ),需要选择合适的滤光片及其厚度,使其光谱透射比τ(λ)与探测器的相对光谱灵敏度S(λ)的组合结果,满足卢瑟条件的要求。下图是采用光学滤色片法实现卢瑟条件的光电积分式色度计的基本构成示意。这种类型的色度计构造简单,成本较低,因此在工业生产中得到广泛的应用。
色差仪卢瑟条件对精度的影响:
色差仪的精度与其光谱特性符合卢瑟条件的程度有关。一般,在色差仪探测器的光谱修正中,要使仪器完全符合卢瑟条件是不可能的,只能是近似匹配。为了减少光探测器光谱修正不完善所带来的误差,应该根据待测样品的颜色,选用不同的标准色板或标准滤色片来校正测色仪器。将选定的标准色板或标准滤色片放入仪器,并调节仪器的输出结果,使测得的三刺激值与标准色板或标准滤色片的定标值一致,然后仪器才能用于实际测试。通常,色差仪配有4~10块不同颜色的标准色板或标准滤色片,其三刺激值由高精度分光光度计预先标定。如果被测的反射或透射色样与校正用标准色板或标准滤色片的颜色相近,则可以认为两者具有近似的光谱反射或透射特性,这时色差仪测得的色度参数就有较高的可靠性。






